Fast and Efficient MMD-based Fair PCA via Optimization over Stiefel Manifold
Abstract
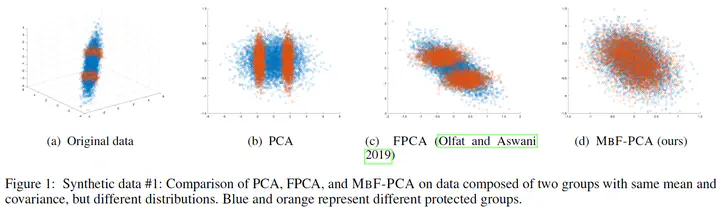
This paper defines fair principal component analysis (PCA) as minimizing the maximum mean discrepancy (MMD) between dimensionality-reduced conditional distributions of different protected classes. The incorporation of MMD naturally leads to an exact and tractable mathematical formulation of fairness with good statistical properties. We formulate the problem of fair PCA subject to MMD constraints as a non-convex optimization over the Stiefel manifold and solve it using the Riemannian Exact Penalty Method with Smoothing (REPMS; Liu and Boumal, 2019). Importantly, we provide local optimality guarantees and explicitly show the theoretical effect of each hyperparameter in practical settings, extending previous results. Experimental comparisons based on synthetic and UCI datasets show that our approach outperforms prior work in explained variance, fairness, and runtime.
(To be filled out)
Junghyun Lee
PhD Student
PhD student at GSAI, KAIST, jointly advised by Prof. Se-Young Yun and Prof. Chulhee Yun. Interested in mathematical and theoretical AI, where I am interested in explaining the recent success of machine/deep learning algorithms and designing mathematically well-grounded algorithms for various scenarios.