Abstract
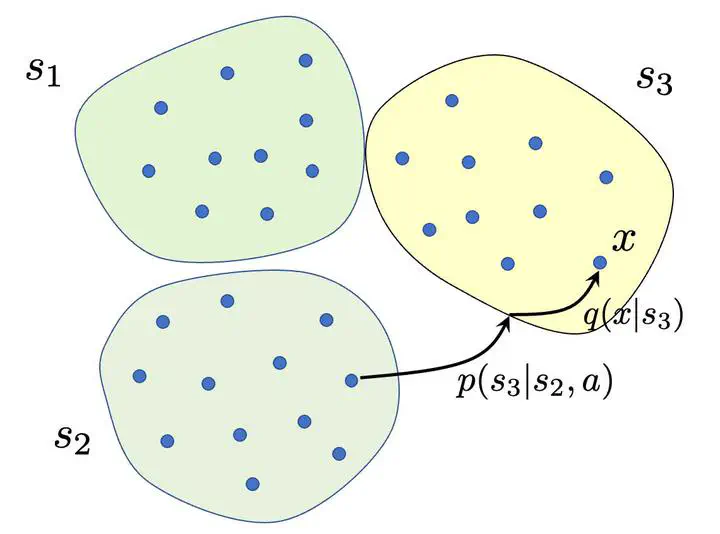
We investigate the problems of model estimation and reward-free learning in episodic Block MDPs. In these MDPs, the decision maker has access to rich observations or contexts generated from a small number of latent states. We are first interested in estimating the latent state decoding function (the mapping from the observations to latent states) based on data generated under a fixed behavior policy. We derive an information-theoretical lower bound on the error rate for estimating this function and present an algorithm approaching this fundamental limit. In turn, our algorithm also provides estimates of all the components of the MDP. We then study the problem of learning near-optimal policies in the reward-free framework. Based on our efficient model estimation algorithm, we show that we can infer a policy converging (as the number of collected samples grows large) to the optimal policy at the best possible rate. Interestingly, our analysis provides necessary and sufficient conditions under which exploiting the block structure yields improvements in the sample complexity for identifying near-optimal policies. When these conditions are met, the sample complexity in the minimax reward-free setting is improved by a multiplicative factor n, where n is the number of possible contexts.
(To be filled out)
Junghyun Lee
PhD Student
PhD student at GSAI, KAIST, jointly advised by Prof. Se-Young Yun and Prof. Chulhee Yun. Interested in mathematical and theoretical AI, where I am interested in explaining the recent success of machine/deep learning algorithms and designing mathematically well-grounded algorithms for various scenarios.