Abstract
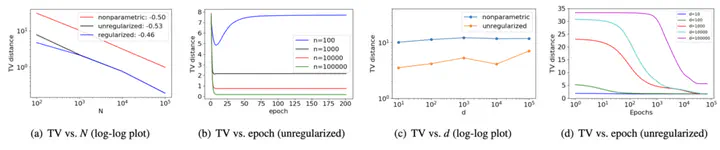
Linear softmax parametrization (LSP) of a discrete probability distribution is ubiquitous in many areas, such as deep learning, RL, NLP, and social choice models. Instead of trying to estimate the unknown parameter as done previously, we consider the problem of estimating a distribution with an LSP. We first provide some theoretical analyses of LSP on its expressivity and nonidentifiability issue, which shows that the error rate cannot be inferred from the classical statistical theory. Then, we empirically show that the solution found by gradient descent on negative log-likelihood objective function results in the same asymptotic rate as the nonparametric estimator but with a smaller multiplicative coefficient.
(To be filled out)
Junghyun Lee
PhD Student
PhD student at GSAI, KAIST, jointly advised by Prof. Se-Young Yun and Prof. Chulhee Yun. Interested in mathematical and theoretical AI, where I am interested in explaining the recent success of machine/deep learning algorithms and designing mathematically well-grounded algorithms for various scenarios.