A Unified Confidence Sequence for Generalized Linear Models, with Applications to Bandits

Abstract

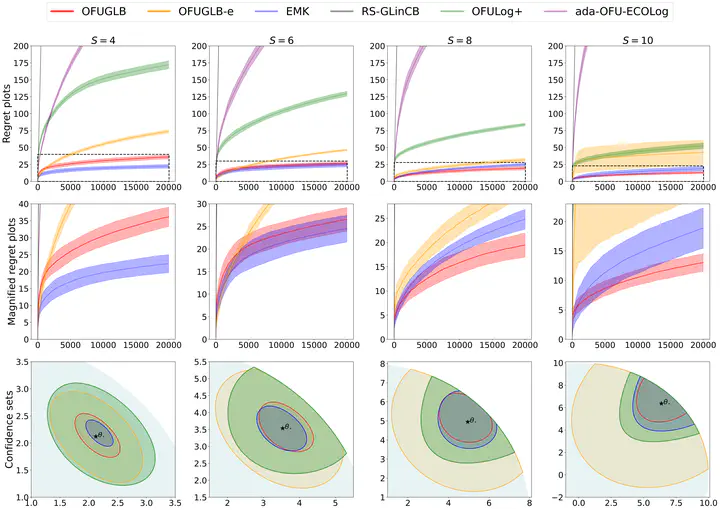
We present a unified likelihood ratio-based confidence sequence (CS) for any (self-concordant) generalized linear model (GLM) that is guaranteed to be convex and numerically tight. We show that this is on par or improves upon known CSs for various GLMs, including Gaussian, Bernoulli, and Poisson. In particular, for the first time, our CS for Bernoulli has a $\mathrm{poly}(S)$-free radius where $S$ is the norm of the unknown parameter. Our first technical novelty is its derivation, which utilizes a time-uniform PAC-Bayesian bound with a uniform prior/posterior, despite the latter being a rather unpopular choice for deriving CSs. As a direct application of our new CS, we propose a simple and natural optimistic algorithm called OFUGLB, applicable to any generalized linear bandits (GLB; Filippi et al. (2010)). Our analysis shows that the celebrated optimistic approach simultaneously attains state-of-the-art regrets for various self-concordant (not necessarily bounded) GLBs, and even $\mathrm{poly}(S)$-free for bounded GLBs, including logistic bandits. The regret analysis, our second technical novelty, follows from combining our new CS with a new proof technique that completely avoids the previously widely used self-concordant control lemma (Faury et al., 2020, Lemma 9). Numerically, OFUGLB outperforms or is at par with prior algorithms for logistic bandits.

Junghyun Lee

PhD Student

PhD student at GSAI, KAIST, jointly advised by Prof. Se-Young Yun and Prof. Chulhee Yun. Interested in mathematical and theoretical AI, i.e., essentially any machine learning challenges necessitating mathematical analysis. Recently focused on statistical problems arising from RLHF, including interactive machine learning and low-dimensional structure recovery.